Earth's magnetic field
Generation of the Earth's magnetic field
Learn about the Earth's magnetic field.
Magnetic charts
Links to magnetic declination, inclination, and total field charts.
Magnetic components
Information about the various components used to represent the magnetic field.
Magnetic declination
Learn about the direction of the magnetic field (i.e. where a compass points).
Magnetic reference field models
Description of the different magnetic field reference models.
Magnetic field in the Arctic regions
Learn about the magnetic field in the vicinity of the north magnetic pole.
Secular variation
Learn about the slow variations of the magnetic field on timescales from years to millennia.
Using a compass
How to use a compass and apply the proper corrections.
Selected Bibliography
Geomagnetism bibliography.
The magnetic field of the Earth (geomagnetic field) resembles the field produced by a simple bar magnet. Such a field is called a dipole field because it has two poles, located at either end of the magnet, where the strength of the field is maximum. At the midpoint between the poles the strength is half of its value at the poles. The magnetic field is often visualized in terms of magnetic field lines, or lines of force, that leave one end of the magnet, called the north pole, arc through space, and re-enter the magnet at the other end, the south pole.
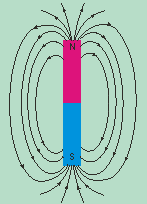
Magnetic field line
If we could place a bar magnet inside the Earth, inclined approximately 11° to the rotational axis and offset about 550 km from the Earth's centre we could account for 90% of the observed magnetic field. We could account for the remaining 10% by placing smaller bar magnets at strategic locations around the primary magnet.
Although this simple description provides a way of conceptualizing the magnetic field it does not represent what really goes inside the Earth. Nor can it be used to calculate the strength and direction of the magnetic field. Mathematically, the Earth's magnetic field is normally described by a spherical harmonic expansion, a series of special spherical functions of latitude/longitude and their associated coefficients. Each group of functions describes a particular field pattern: the first three terms describe the field of a dipole; the next 5 terms describe a quadrapole field; the following 7 terms describe an octopole field. By adjusting the relative size of each of these component parts the shape of the actual field can be closely approximated.
Such mathematical descriptions of the magnetic field are called magnetic reference field models. The most widely used reference field model is the International Geomagnetic Reference Field (IGRF). The IGRF is produced every five years under the auspices of the International Association of Geomagnetism and Aeronomy (IAGA).